多重ループ探索→再帰呼び出し/アルゴリズム講座

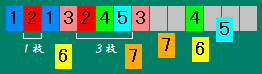
第２章(1): 多重ループ探索

　先ほどの虫食い算に習って、今度はこの問題を解いてみましょう。

　例題３: 2枚のカードの間には？

　1から7の数字を書いたカードが2枚ずつ計14枚ある。そしてこれを1列に並べ，2枚の1の間にはカードが1枚，2枚の2の間にはカードが2枚はさまれていて,同様に，3の間には3枚,4の間には4枚,5の間には5枚,6の間には6枚,7の間には7枚のカードがはさまれるように14枚のカードを並べて下さい。

(Ｃマガ電脳クラブ91年4月号より)

　基本方針として、[１]のカードからペアで順番に配置していき、また、左側への可能な配置から順次試していくことにします。

　さて、前回は未知数が２つだったのでfor文を二重に重ねましたが、今回は7種類のカードの位置が未知数なのでfor文を７重に重ねることになります。List.2-1

　このように未知数の数だけfor文を重ねれば全パターンを調べることが出来ます。もし未知数が20個あればfor文を20個重ねることになります。
　しかし、これは大変です。もっといい方法は無いものでしょうか。ほとんどのプログラム言語には「再帰呼び出し」という便利な機能があって、for文をたくさん重ねなくとも、もっと簡潔にプログラムを書く方法があるのです。

第２章(2): 再帰呼び出し

　あなたがもし「折半」という言葉の意味を知りたくて国語辞典を調べたとします。すると、こう書いてありました。

　「折半」とは、金銭等を二人で折半すること。

　こんな国語辞典はありません。「折半」を説明するのに「折半」という言葉を使うのはおかしい。でも、プログラミングの世界では、このような記述を可能にしているのです。

nの階乗値を返す関数 List.2-2 をご覧下さい。関数の中で自分自身を呼び出しています。

　そして、４の階乗なら、「４」×「３の階乗」を答えとして返します。一見すると不思議に思えますが、呼び出すときのnの値が異なります。つまり、全く同じものを呼び出しているのでは無いのです。
　自分自身をそのまま呼び出すのではなく、自分の複製を作ってそれを呼び出すと考えると分かり易いかも知れません。List.2-3

　パズル問題をプログラムで解くとき、この「再帰呼び出し」が大活躍します。では、例題３に戻りましょう。

　この再帰呼び出しを使って例題３を解くプログラムは List.2-4 のように簡潔になります。for文は１個しかありませんが、処理の流れを追いかければfor文は７重に実行されます。

　再帰呼び出しを使う上で、大切なポイントが２つあります。

　１．終着点があること

　呼び出しが無限に繰り返されてはなりません。再帰とは再び帰ってくるということ。そのためには終着点が必要になります。nの階乗はn=1が終着点であり、例題３は7枚のカードが配置されたときが終着点となります。

　２．関数を抜けるときは元に戻す

　グローバルな変数を用いて状態を把握している場合、関数を抜けるときは関数に入ったときの状態に必ず戻すようにして下さい。そうしないと探索の整合性が失われてしまいます。

ホームページへ戻る

List.2-1　7重のforループを使う

    // 1のカードを配置
    for (L1=0,R1=2; R1<14; L1++,R1++) {
      TABLE[L1] = TABLE[R1] = 1;        // 置く
      // 2のカードを配置
      for (L2=0,R2=3; R2<14; L2++,R2++) {
        if (TABLE[L2]==0 && TABLE[R2]==0) { // 置けるなら
          TABLE[L2] = TABLE[R2] = 2;        // 置く
          // 3のカードを配置
          for (L3=0,R3=4; R3<14; L3++,R3++) {
            if (TABLE[L3]==0 && TABLE[R3]==0) {
              TABLE[L3] = TABLE[R3] = 3;
              // 4のカードを配置
              for (L4=0,R4=5; R4<14; L4++,R4++) {

                    ---(省略)---

                    // 7のカードを配置
                    for (L7=0,R7=8; R7<14; L7++,R7++) {
                        if (TABLE[L7]==0 && TABLE[R7]==0) {
                            TABLE[L7] = TABLE[R7] = 7;

                            // TABLE[]を表示する:省略

                            TABLE[L7] = TABLE[R7] = 0;  // 消す
                        }
                    }

                    ---(省略)---

              }
              TABLE[L3] = TABLE[R3] = 0;    // 消す
            }
          }
          TABLE[L2] = TABLE[R2] = 0;    // 消す
        }
      }
      TABLE[L1] = TABLE[R1] = 0;    // 消す
    }

List.2-2　nの階乗を返す関数

int Kaijyo(int n)
{
    if (n < 2) {
        return 1;
    } else {
        return n * Kaijyo(n-1); // 自分を呼び出している
    }
}

List.2-3　4の階乗が求まる実際の流れ

int Kaijyo1()   // nを1に変えて複製された関数
{
    return 1;
}
int Kaijyo2()   // nを2に変えて複製された関数
{
    return 2 * Kaijyo1();
}
int Kaijyo3()   // nを3に変えて複製された関数
{
    return 3 * Kaijyo2();
}
int Kaijyo4()   // n=4の階乗を求める関数
{
    return 4 * Kaijyo3();
}

List.2-4　再帰呼び出しで例題３を解く

int TABLE[14];  // カードを置いていくテーブル

void Card(int n)
{
    int L, R;

    if (n > 7) {    // すべてのカードが置かれた
        // TABLE[]を表示する:省略
    } else {
        // nのカードを配置
        for (L=0,R=n+1; R<14; L++,R++) {
            if (TABLE[L]==0 && TABLE[R]==0) { // 置けるなら
                TABLE[L] = TABLE[R] = n;      // 置く
                Card(n+1);		// 再帰呼び出し
                TABLE[L] = TABLE[R] = 0;      // 消す
            }
        }
    }
}
void Puzzle()
{
    Card(1);     // 最初に1のカードを置く
}