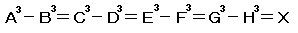一見して奇妙に思うことは、Ｎの上限値が示されていないことですがジックリ分析すると１０桁を超えるＮでは常に[１の個数＞Ｎ]であることが理論的に導き出せます。(ソースリスト内の説明参照)
そこで、for (n = 1; n < 10000000000; n++) の中で題意通りに単純に１の個数を数えるようなプログラム記述が考えられますが、これだと探索を終えるのに相当な時間がかかってしまうようです。
何かいい「枝刈り」はないでしょうか。１の個数はＮが増加するにつれて増えていくだけで減ることは無いはずです。ですから、次のことが言えます。
[1の個数]＞[N]の時、その後のNの値に1を全く含まないと仮定しても、
Nがその時の1の個数の値に達するまでは[1の個数]＝[N]になることは無い。
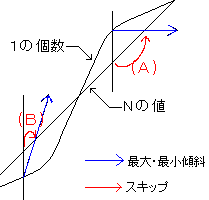
そこで、こんな状態の時は[Nの値]を一気にその時の[1の個数の値]までスキップ出来ます(Ａ)。スキップさせるからには、Nの値からダイレクトにNまでの1の個数を求める関数を用意する必要があります。
これだけで満足してはいけません。[1の個数]＜[N]の時のことも考えましょう。
相反する２つの条件で挟み込むように枝刈りするというのは大変に効果的なのです。
[1の個数]＜[N]の時、その後のNの値が10桁全て1だったと仮定しても、
Nにその差の1/10加算に達するまでは[1の個数]＝[N]になることは無い。
こんな状態の時も[Nの値]を一気に[差の1/10加算値]までスキップさせましょう(Ｂ)。いい枝刈り法が見つかりました。この２つの枝刈りに挟み込まれる様にリードされて一瞬に答えを求めてくれました。
私の応募したソースリスト
この問題は、１０人いれば１０種類のプログラムが登場してもおかしくない程、いろいろなアプローチが考えられますが、私は、多重ループ検索という極めて単純なアルゴリズムを用いましたが....。
01: // A,B,Xの組合せを生成
02: for (A=1; ;A++)
03: for (B=A-1; B; B--) {
04: X = A*A*A - B*B*B;
05:
06: // C,Dの組合せを探す
07: for (C,Dの組をA,Bの降方に探す) {
08:
09: // E,Fの組合せを探す
10: for (E,Fの組をC,Dの降方に探す) {
11:
12: // G,Hの組合せを探す
13: for (G,Hの組をE,Fの降方に探す) {
14:
15: // A,B,...H,Xを記録;
16: }
17: }
18: }
19: }
これで、当時の私の環境では約６秒で答えを出しました。しかし、HASH[HSIZE] という大きなテーブルを用意しておき、５行目に次の１文を付加してやると、探索は０.２秒で終了しました。たった１行追加するだけの驚くべき高速化でした。
05: if (++HASH[X%HSIZE] < 4) continue;
これは、Xの出現回数をハッシュ値でカウントしています。再ハッシュ計算などしないので、大まかなカウントなのですが、４通りの組が存在する可能性(期待)をチェックするだけなら、これで充分なのです。
私の応募したソースリスト
正方形５個を辺同士でつなげてできた図形をペントミノといい、１２種類のそれぞれに呼び名がついている。