| ・完了型から初期型に向かう逆解きを採用 |
|
初期型から探索を開始する通常の探索法では、倉庫番を解くVer2.7に示したように
多くの枝刈りを組み込まないと無駄な探索が大量に発生してしまいます。
しかし、逆解きでの間違った手順は、自分を閉じ込めて探索を収束させる場合が多く、枝刈りはほぼ不要になります。
| 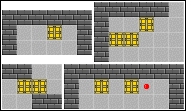
通常解きでの失敗例 | 
逆解きでの失敗例 |
| ・1回の動作の概念について |
|
最短歩数の解を求めるのであれば、1回の動作の概念は1歩であるべきですが、無駄に動き回る局面は不要なので、「目的の荷物の手前まで最短で歩き1回だけ荷物を引く」という動作を1回の動作としています。それだと
最短歩数では無く、最小荷押し数(minimum pushes)の解が求まってしまうのでは無いか? いいえ、そうはならない秘策を次の項で述べます。
| 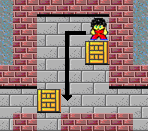
【親局面】最短で歩き、 | 
【子局面】1回引く |
| ・二次元キューを使った幅優先探索 |
|
このプログラムは、基本的に「第4章: 幅優先探索」を使っています。しかし、待ち行列(キュー)が1個では無くたくさんあります。上図の例では、親局面から子局面まで5歩使っています。この場合は、n歩用のキューから親局面を取り出して、子局面はn+5歩用のキューに登録します。n歩用のキューが空になれば、n+1歩用のキューからの取り出しに移行します。
| 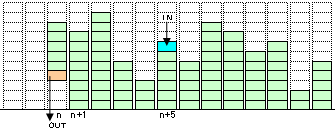
nから親局面を取り出し、子局面をn+5に登録 |
| ・トンネル内での枝刈り |
|
トンネルとは、幅1マスの直線通路のことです。このトンネル内に荷物を一旦放置する局面は、
最短歩数の解には絶対に到達しないので、子局面として登録しません。(右図参照)
|
初期状態 
|
放置禁止 
|
| ・マトリックス枝刈り |
|
N個の荷物とN個のゴールでN組のカップルが成立するかを調べます。例えば荷物が4個(荷物A、荷物B、荷物C、荷物D)あるとして、ある位置pos1には荷物Aしか運べない場合は、Bits[pos1] = 1000 (2進法)とし、位置pos2の場合は、荷物A、荷物B、荷物Dの3つが運べるのなら、Bits[pos2] = 1101 (2進法) として、総てのマスについて荷物を運べる状況(Bits[])を事前に調べておきます。
|
|
逆解き探索中は、4つの荷物(荷物1、荷物2、荷物3、荷物4)の各位置のBits[]の値を右図のように並べてマトリックスを作ります。このマトリックスをN飛車問題(Nクイーン問題の飛車バージョン)として解が存在するかを調べます。
|
Bits[荷物1位置] = 1000
Bits[荷物2位置] = 1101
Bits[荷物3位置] = 0111
Bits[荷物4位置] = 0110
|